Modular Multiplicative Inverse

The modular multiplicative inverse of an integer a modulo m is an integer x such that

That is, it is the multiplicative inverse in the ring of integers modulo m. This is equivalent to

The multiplicative inverse of a modulo m exists if and only if a and m are coprime (i.e., if gcd(a, m) = 1).

Let’s see various ways to calculate Modular Multiplicative Inverse:

1. Brute Force
We can calculate the inverse using a brute force approach where we multiply a with all possible values x and find a x such that Here’s a sample C++ code:

int modInverse(int a, int m) {
	a %= m;
	for(int x = 1; x < m; x++) {
		if((a*x) % m == 1) return x;
	}
}

The time complexity of the above codes is O(m).

2. Using Extended Euclidean Algorithm
We have to find a number x such that a·x = 1 (mod m). This can be written as well as a·x = 1 + m·y, which rearranges into a·x – m·y = 1. Since x and y need not be positive, we can write it as well in the standard form, a·x + m·y = 1.

In number theory, Bézout’s identity for two integers a, b is an expression ax + by = d, where x and y are integers (called Bézout coefficients for (a,b)), such that d is a common divisor of a and b. If d is the greatest common divisor of a and b then Bézout’s identity ax + by = gcd(a,b) can be solved using Extended Euclidean Algorithm.

The Extended Euclidean Algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y (one of which is typically negative) that satisfy Bézout’s identity
ax + by = gcd(a,b). The Extended Euclidean Algorithm is particularly useful when a and b are coprime, since x is the multiplicative inverse of a modulo b, and y is the multiplicative inverse of b modulo a.

We will look at two ways to find the result of Extended Euclidean Algorithm.

Iterative Method
This method computes expressions of the form r_i = ax_i + by_i for the remainder in each step i of the Euclidean algorithm. Each successive number r_i can be written as the remainder of the division of the previous two such numbers, which remainder can be expressed using the whole quotient q_i of that division as follows:

By substitution, this gives:
which can be written

The first two values are the initial arguments to the algorithm:


So the coefficients start out as x₁ = 1, y₁ = 0, x₂ = 0, and y₂ = 1, and the others are given by


The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.

So the algorithm looks like,

1. Apply Euclidean algorithm, and let qn(n starts from 1) be a finite list of quotients in the division.
2. Initialize x₀, x₁ as 1, 0, and y₀, y₁ as 0,1 respectively.
   1. Then for each i so long as q_i is defined,
   2. Compute x_i+1 = x_i-1 − q_ix_i
   3. Compute y_i+1 = y_i-1 − q_iy_i
   4. Repeat the above after incrementing i by 1.
3. The answers are the second-to-last of x_n and y_n.

/* This function return the gcd of a and b followed by
	the pair x and y of equation ax + by = gcd(a,b)*/
pair<int, pair<int, int> > extendedEuclid(int a, int b) {
	int x = 1, y = 0;
	int xLast = 0, yLast = 1;
	int q, r, m, n;
	while(a != 0) {
		q = b / a;
		r = b % a;
		m = xLast - q * x;
		n = yLast - q * y;
		xLast = x, yLast = y;
		x = m, y = n;
		b = a, a = r;
	}
	return make_pair(b, make_pair(xLast, yLast));
}

int modInverse(int a, int m) {
    return (extendedEuclid(a,m).second.first + m) % m;
}

Recursive Method
This method attempts to solve the original equation directly, by reducing the dividend and divisor gradually, from the first line to the last line, which can then be substituted with trivial value and work backward to obtain the solution.
Notice that the equation remains unchanged after decomposing the original dividend in terms of the divisor plus a remainder, and then regrouping terms. So the algorithm looks like this:

1. If b = 0, the algorithm ends, returning the solution x = 1, y = 0.
2. Otherwise:
   • Determine the quotient q and remainder r of dividing a by b using the integer division algorithm.
   • Then recursively find coefficients s, t such that bs + rt divides both b and r.
   • Finally the algorithm returns the solution x = t, and y = s − qt.

Here’s a C++ implementation:

/* This function return the gcd of a and b followed by
	the pair x and y of equation ax + by = gcd(a,b)*/
pair<int, pair<int, int> > extendedEuclid(int a, int b) {
	if(a == 0) return make_pair(b, make_pair(0, 1));
	pair<int, pair<int, int> > p;
	p = extendedEuclid(b % a, a);
	return make_pair(p.first, make_pair(p.second.second - p.second.first*(b/a), p.second.first));
}

int modInverse(int a, int m) {
    return (extendedEuclid(a,m).second.first + m) % m;
}

The time complexity of the above codes is O(log(m)²).

3. Using Fermat’s Little Theorem
Fermat’s little theorem states that if m is a prime and a is an integer co-prime to m, then a^p − 1 will be evenly divisible by m. That is or Here’s a sample C++ code:

/* This function calculates (a^b)%MOD */
int pow(int a, int b, int MOD) {
int x = 1, y = a;
	while(b > 0) {
		if(b%2 == 1) {
			x=(x*y);
			if(x>MOD) x%=MOD;
		}
		y = (y*y);
		if(y>MOD) y%=MOD;
		b /= 2;
	}
	return x;
}

int modInverse(int a, int m) {
    return pow(a,m-2,m);
}

The time complexity of the above codes is O(log(m)).

4. Using Euler’s Theorem
Fermat’s Little theorem can only be used if m is a prime. If m is not a prime we can use Euler’s Theorem, which is a generalization of Fermat’s Little theorem. According to Euler’s theorem, if a is coprime to m, that is, gcd(a, m) = 1, then , where where φ(m) is Euler Totient Function. Therefore the modular multiplicative inverse can be found directly: . The problem here is finding φ(m). If we know φ(m), then it is very similar to above method.

---

Now lets take a little different question. Now suppose you have to calculate the inverse of first n numbers. From above the best we can do is O(n log(m)). Can we do any better? Yes.

We can use sieve to find a factor of composite numbers less than n. So for composite numbers inverse(i) = (inverse(i/factor(i)) * inverse(factor(i))) % m, and we can use either Extended Euclidean Algorithm or Fermat’s Theorem to find inverse for prime numbers. But we can still do better.

a * (m / a) + m % a = m
(a * (m / a) + m % a) mod m = m mod m, or
(a * (m / a) + m % a) mod m = 0, or
(- (m % a)) mod m = (a * (m / a)) mod m.
Dividing both sides by (a * (m % a)), we get
– inverse(a) mod m = ((m/a) * inverse(m % a)) mod m
inverse(a) mod m = (- (m/a) * inverse(m % a)) mod m

Here’s a sample C++ code:

vector<int> inverseArray(int n, int m) {
	vector<int> modInverse(n + 1,0);
	modInverse[1] = 1;
	for(int i = 2; i <= n; i++) {
		modInverse[i] = (-(m/i) * modInverse[m % i]) % m + m;
	}
	return modInverse;
}

The time complexity of the above code is O(n).

-fR0DDY

Knuth–Morris–Pratt Algorithm (KMP)

Knuth–Morris–Pratt algorithm is the most popular linear time algorithm for string matching. It is little difficult to understand and debug in real time contests. So most programmer’s have a precoded KMP in their kitty.

To understand the algorithm, you can either read it from Introduction to Algorithms (CLRS) or from the wikipedia page. Here’s a sample C++ code.

void preKMP(string pattern, int f[])
{
        int m = pattern.length(),k;
        f[0] = -1;
        for (int i = 1; i<m; i++)
        {
                k = f[i-1];
                while (k>=0)
                {
                        if (pattern[k]==pattern[i-1])
                                break;
                        else
                                k = f[k];
                }
                f[i] = k + 1;
        }
}
 
bool KMP(string pattern, string target)
{ 
        int m = pattern.length();
        int n = target.length();
        int f[m];
        
        preKMP(pattern, f);
        
        int i = 0;
        int k = 0;
        
        while (i<n)
        {
                if (k==-1)
                {
                        i++;
                        k = 0;
                }
                else if (target[i]==pattern[k])
                {
                        i++;
                        k++;
                        if (k==m)
                                return 1;
                }
                else
                        k=f[k];
        }
        return 0;
}

NJOY!
-fR0DDY

The Z Algorithm

In this post we will discuss an algorithm for linear time string matching. It is easy to understand and code and is usefull in contests where you cannot copy paste code.

Let our string be denoted by S.
z[i] denotes the length of the longest substring of S that starts at i and is a prefix of S.
α denotes the substring.
r denotes the index of the last character of α and l denotes the left end of α.

To find whether a pattern(P) of length n is present in a target string(T) of length m, we will create a new string S = P$T where $ is a character present neither in P nor in T. The space taken is n+m+1 or O(m). We will compute z[i] for all i such that 0 < i < n+m+1. If z[i] is equal to n then we have found a occurrence of P at position i – n – 1. So we can all the occurrence of P in T in O(m) time. To calculate z[i] we will use the z algorithm.

The Z Algorithm can be read from the section 1.3-1.5 of book Algorithms on strings, trees, and sequences by Gusfield. Here is a sample C++ code.

bool zAlgorithm(string pattern, string target)
{
	string s = pattern + '$' + target ;
	int n = s.length();
	vector<int> z(n,0);
	
	int goal = pattern.length();
	int r = 0, l = 0, i;
	for (int k = 1; k<n; k++)
	{
		if (k>r)
		{
			for (i = k; i<n && s[i]==s[i-k]; i++);
			if (i>k)
			{
				z[k] = i - k;
				l = k;
				r = i - 1;
			}
		}
		else
		{
			int kt = k - l, b = r - k + 1;
			if (z[kt]>b)
			{
				for (i = r + 1; i<n && s[i]==s[i-k]; i++);
				z[k] = i - k;
				l = k;
				r = i - 1;
			}
		}
		if (z[k]==goal)
			return true;
	}
	return false;
}

NJOY!
-fR0D

Longest Common Increasing Subsequence (LCIS)

Given 2 sequences of integers, we need to find a longest sub-sequence which is common to both the sequences, and the numbers of such a sub-sequence are in strictly increasing order.
For example,
2 3 1 6 5 4 6
1 3 5 6
the LCIS is 3 5 6.

The sequence a₁, a₂, …, a_n is called increasing, if a_i<a_i+1 for i<n.The sequence s₁, s₂, …, s_k is called the subsequence of the sequence a₁, a₂, …, a_n, if there exist such a set of indexes 1 ≤ i₁ < i₂ < … < i_k ≤ n that a_ij = s_j. In other words, the sequence s can be derived from the sequence a by crossing out some elements.

A nice tutorial on the algorithm is given on CodeChef blog here. If you read the blog you can see that instead of looking for LCIS in a candidate matrix, we can keep an array that stores the length of LCIS ending at that particular element. Also we keep a lookup previous array that gives the index of the previous element of the LCIS, which is used to reconstruct the LCIS.

For every element in the two arrays
1> If they are equal we check whether the LCIS formed will be bigger than any previous such LCIS ending at that element. If yes we change the data.
2> If the jth element of array B is smaller than ith element of array A, we check whether it has a LCIS greater than current LCIS length, if yes we store it as previous value and it’s LCIS length as current LCIS length.

Here’s a C++ code.

#include<iostream>
using namespace std;
#include<vector>

void LCIS(vector<int> A, vector<int> B)
{
    int N=A.size(),M=B.size(),i,j;
    vector<int> C(M,0);
    vector<int> prev(M,0);
    vector<int> res;
    
    for (i=0;i<N;i++)
    {
        int cur=0,last=-1;
        for (j=0;j<M;j++)
        {
            if (A[i]==B[j] && cur+1>C[j])
            {
               C[j]=cur+1;
               prev[j]=last;
            }
            if (B[j]<A[i] && cur<C[j])
            {
               cur=C[j];
               last=j;
            }
        }
    }
    
    int length=0,index=-1;
    for (i=0;i<M;i++)
        if (C[i]>length)
        {
           length=C[i];
           index=i;
        }
    printf("The length of LCIS is %d\n",length);
    if (length>0)
    {
       printf("The LCIS is \n");
       while (index!=-1)
       {
             res.push_back(B[index]);
             index=prev[index];
       }
       reverse(res.begin(),res.end());
       for (i=0;i<length;i++)
           printf("%d%s",res[i],i==length-1?"\n":" ");
    }
}


int main()
{
    int n,m,i;
    scanf ("%d", &n);
    vector<int> A(n,0);
    for (i = 0; i < n; i++)
        scanf ("%d", &A[i]);
    scanf ("%d", &m);
    vector<int> B(m,0);
    for (i = 0; i < m; i++)
        scanf ("%d", &B[i]);
    LCIS(A,B);
}

NJOY!
-fR0DDY

Number of Binary Trees

Question : What is the number of rooted plane binary trees with n nodes and height h?

Solution :
Let t_n,h denote the number of binary trees with n nodes and height h.

Lets take a binary search tree of n nodes with height equal to h. Let the number written at its root be the m^thnumber in sorted order, 1 ≤ m ≤ n. Therefore, the left subtree is a binary search tree on m-1 nodes, and the right subtree is a binary search tree on n-m nodes. The maximum height of the left and the right subtrees must be equal to h-1. Now there are two cases :

1. The height of left subtree is h-1 and the height of right subtree is less than equal to h-1 i.e from 0 to h-1.
2. The height of right subtree is h-1 and the height of left subtree is less than equal to h-2 i.e from 0 to h-2, since we have considered the case when the left and right subtrees have the same height h-1 in case 1.

Therefore t_n,h is equal to the sum of number of trees in case 1 and case 2. Let’s find the number of trees in case 1 and case 2.

1. The height of the left subtree is equal to h-1. There are t_m-1,h-1 such trees. The right subtree can have any height from 0 to h-1, so there are such trees. Therefore the total number of such tress are .
2. The height of the right subtree is equal to h-1. There are t_n-m,h-1 such trees. The left subtree can have any height from 0 to h-2, so there are such trees. Therefore the total number of such tress are .

Hence we get the recurrent relation

or

where t_0,0=1 and t_0,i=t_i,0=0 for i>0.
Here’s a sample C++ code.

#include<iostream>
using namespace std;

#define MAXN 35

int main()
{
    long long t[MAXN+1][MAXN+1]={0},n,h,m,i;
    
    t[0][0]=1;
    for (n=1;n<=MAXN;n++)
        for (h=1;h<=n;h++)
            for (m=1;m<=n;m++)
            {
                for (i=0;i<h;i++)
                    t[n][h]+=t[m-1][h-1]*t[n-m][i];
                
                for (i=0;i<h-1;i++)
                    t[n][h]+=t[n-m][h-1]*t[m-1][i];
            }
            
    while (scanf("%lld%lld",&n,&h))
          printf("%lld\n",t[n][h]);
}

Note :

1. The total number of binary trees with n nodes is , also known as Catalan numbers or Segner numbers.
2. t_n,n = 2^n-1.
3. The number of trees with height not lower than h is .
4. There are other recurrence relation as well such as
   .

NJOY!
-fR0DDY

Convert a number from decimal base to any Base

Convert a given decmal number to any other base (either positive or negative).

For example, 100 in Base 2 is 1100100 and in Base -2 is 110100100.

Here’s a simple algorithm to convert numbers from Decimal to Negative Bases :

def tonegativeBase(N,B):
   digits = []
   while i != 0:
	i, remainder = divmod (i, B)
	if (remainder < 0):
	    i, remainder = i + 1, remainder + B*-1
	digits.insert (0, str (remainder))
   return ''.join (digits)

We can just tweak the above algorithm a bit to convert a decimal to any Base. Here’s a sample code :

#include<iostream>
using namespace std;

void convert10tob(int N,int b)
{
     if (N==0)
        return;
     
     int x = N%b;
     N/=b;
     if (x<0)
        N+=1;
        
     convert10tob(N,b);
     printf("%d",x<0?x+(b*-1):x);
     return;
}


int main()
{
    int N,b;
    while (scanf("%d%d",&N,&b)==2)
    {
          if (N!=0)
          {
              convert10tob(N,b);
              printf("\n");
          }
          else
              printf("0\n");
    }
}

NJOY!
-fR0DDY

Number of zeores and digits in N Factorial in Base B

Question : What is the number of trailing zeroes and the number of digits in N factorial in Base B.

For example,
20! can be written as 2432902008176640000 in decimal number system while it is equal to “207033167620255000000” in octal number system and “21C3677C82B40000” in hexadecimal number system. That means that 10 factorial has 4 trailing zeroes in Base 10 while it has 6 trailing zeroes in Base 8 and 4 trailing zeroes in Base 16. Also 10 factorial has 19 digits in Base 10 while it has 21 digits in Base 8 and 16 digits in Base 16. Now the question remains how to find it?

Now we can break the Base B as a product of primes :
B = a^p1 * b^p2 * c^p3 * …
Then the number of trailing zeroes in N factorial in Base B is given by the formulae
min{1/p1(n/a + n/(a*a) + ….), 1/p2(n/b + n/(b*b) + ..), ….}.

And the number of digits in N factorial is :
floor (ln(n!)/ln(B) + 1)

Here’s a sample C++ code :

#include<iostream>
using namespace std;
#include<math.h>

int main()
{
    int N,B,i,j,p,c,noz,k;
    while (scanf("%d%d",&N,&B)!=EOF)
    {
          noz=N;
          j=B;
          for (i=2;i<=B;i++)
          {
              if (j%i==0)
              {   
                 p=0;
                 while (j%i==0)
                 {
                       p++;
                       j/=i;
                 }
                 c=0;
                 k=N;
                 while (k/i>0)
                 {
                       c+=k/i;
                       k/=i;
                 }
                 noz=min(noz,c/p);
              }
          }
          double ans=0;
          for (i=1;i<=N;i++)
          {
              ans+=log(i);
          }
          ans/=log(B);ans+=1.0;
          ans=floor(ans);
          printf("%d %.0lf\n",noz,ans);
    }
}

NJOY!
-fR0DDY

Number of Distinct LCS

This problem appeared in the November edition of CodeChef Monthly Contest. The problem is to find the number of distinct LCS that can be formed from the given two strings. A nice tutorial about it is given on the CodeChef site itself. Also there is a research paper available here. Here’s my solution to the CodeChef problem.

#include<iostream>
using namespace std;

int L[1005][1005];
int D[1005][1005];

int LCS(string X,string Y)
{
     int m = X.length(),n=Y.length();
     
     int i,j;
     for (i=0;i<=m;i++)
     {
         for (j=0;j<=n;j++)
         {
             if (i==0 || j==0)
                L[i][j]=0;
             else
             {
                 if (X[i-1]==Y[j-1])
                    L[i][j]=L[i-1][j-1]+1;
                 else
                     L[i][j]=max(L[i][j-1],L[i-1][j]);
             }
         }
     }
     return (L[m][n]);
}

int NLCS(string X,string Y)
{
    int m = X.length(),n=Y.length();
    int i,j;
    for (i=0;i<=m;i++)
    {
        for (j=0;j<=n;j++)
        {
             if (i==0 || j==0)
                D[i][j]=1;
             else
             {
                 D[i][j]=0;
                 if (X[i-1]==Y[j-1])
                 {
                    D[i][j]=D[i-1][j-1];
                 }
                 else
                 {
                     if (L[i-1][j]==L[i][j]) 
                        D[i][j]=(D[i][j]+D[i-1][j])%23102009;
                     if (L[i][j-1]==L[i][j]) 
                        D[i][j]=(D[i][j]+D[i][j-1])%23102009;
                     if (L[i-1][j-1]==L[i][j]) 
                     {
                        if (D[i][j]<D[i-1][j-1])
                           D[i][j]+=23102009;
                        D[i][j]=(D[i][j]-D[i-1][j-1]);
                     }
                 }
             }
        }
     }
     return (D[m][n]);
}

int main()
{
    string X,Y;
    int T,A,B;
    scanf("%d",&T);
    while (T--)
    {
          cin>>X>>Y;
          A=LCS(X,Y);
          B=NLCS(X,Y);
          printf("%d %d\n",A,B);
    }
}

NJOY!
-fR0DDY

Binary Indexed Tree (BIT)

In this post we will discuss the Binary Indexed Trees structure. According to Peter M. Fenwick, this structure was first used for data compression. Let’s define the following problem: We have n boxes. Possible queries are

1. Add marble to box i
2. Return sum of marbles from box k to box l

The naive solution has time complexity of O(1) for query 1 and O(n) for query 2. Suppose we make m queries. The worst case (when all queries are 2) has time complexity O(n * m). Binary Indexed Trees are easy to code and have worst time complexity O(m log n).

The two major functions are

• update (idx,val) : increases the frequency of index idx with the value val
• read (idx) : reads the cumulative frequency of index idx

Note : tree[idx] is sum of frequencies from index (idx – 2^r + 1) to index idx where r is rightmost position of 1 in the binary notation of idx, f is frequency of index, c is cumulative frequency of index, tree is value stored in tree data structure.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
f	1	0	2	1	1	3	0	4	2	5	2	2	3	1	0	2
c	1	1	3	4	5	8	8	12	14	19	21	23	26	27	27	29
tree	1	1	2	4	1	4	0	12	2	7	2	11	3	4	0	29

Table 1.1

 

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
tree	1	1..2	3	1..4	5	5..6	7	1..8	9	9..10	11	9..12	13	13..14	15	1..16

Table 1.2 – table of responsibility

Here’s a C++ template code :

#include<iostream>
using namespace std;

template<class T>
class BIT
{
      T *tree;
      int maxVal;
      public:
      BIT(int N)
      {
              tree = new T[N+1];
              memset(tree,0,sizeof(T)*(N+1));
              maxVal = N;
      }
      void update(int idx, T val)
      {
           while (idx <= maxVal)
           {
                 tree[idx] += val;
                 idx += (idx & -idx);
           }
      }
      //Returns the cumulative frequency of index idx
      T read(int idx)
      {
        T sum=0;
        while (idx>0)
        {
              sum += tree[idx];
              idx -= (idx & -idx);
        }
        return sum;
      }
};

int main()
{
    int a[100],cur=1,mul=2,add=19,MAX=65536,x,i;
    //Initialize the size by the
    //maximum value the tree can have
    BIT<int> B(MAX);
    for (i=0;i<50;i++)
    {
        a[i] = cur;
        B.update(a[i],1);
        cur = ((cur * mul + add) % MAX);
    }
    while (cin>>x)
    {
          cout<<B.read(x)<<endl;
    }

}

Resources:

1. Topcoder Tutorial

NJOY!
-fR0D

Segment Trees

A segment tree is a heap-like data structure that can be used for making update/query operations upon array intervals in logarithmical time. We define the segment tree for the interval [i, j] in the following recursive manner:

• the first node will hold the information for the interval [i, j]
• if i<j the left and right son will hold the information for the intervals [i, (i+j)/2] and [(i+j)/2+1, j]

See the picture below to understand more :

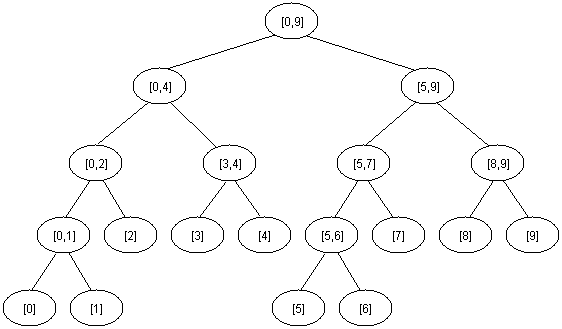
Segment Tree

We can use segment trees to solve Range Minimum/Maximum Query Problems (RMQ). The time complexity is T(N, log N) where O(N) is the time required to build the tree and each query takes O(log N) time. Here’s a C++ template implementation :

#include<iostream>
using namespace std;
#include<math.h>

template<class T>
class SegmentTree
{
     int *A,size;
     public:
     SegmentTree(int N)
     {
          int x = (int)(ceil(log2(N)))+1;
          size = 2*(int)pow(2,x);
          A = new int[size];
          memset(A,-1,sizeof(A));
     }
     void initialize(int node, int start,
                         int end, T *array)
     {

          if (start==end)
             A[node] = start;
          else
          {
              int mid = (start+end)/2;
              initialize(2*node,start,mid,array);
              initialize(2*node+1,mid+1,end,array);
              if (array[A[2*node]]<=
                     array[A[2*node+1]])
                 A[node] = A[2 * node];
              else
                  A[node] = A[2 * node + 1];
          }
     }
     int query(int node, int start,
                   int end, int i, int j, T *array)
     {
         int id1,id2;
         if (i>end || j<start)
            return -1;

         if (start>=i && end<=j)
            return A[node];

         int mid = (start+end)/2;
         id1 = query(2*node,start,mid,i,j,array);
         id2 = query(2*node+1,mid+1,end,i,j,array);

         if (id1==-1)
            return id2;
         if (id2==-1)
            return id1;

         if (array[id1]<=array[id2])
            return id1;
         else
             return id2;
     }
};

int main()
{
    int i,j,N;
    int A[1000];
    scanf("%d",&N);
    for (i=0;i<N;i++)
        scanf("%d",&A[i]);

    SegmentTree<int> s(N);
    s.initialize(1,0,N-1,A);
    while (scanf("%d%d",&i,&j)!=EOF)
      printf("%d\n",A[s.query(1,0,N-1,i-1,j-1,A)]);
}

Resources:

1. Topcoder Tutorial

NJOY!
-fR0D