Knuth–Morris–Pratt Algorithm (KMP)

Knuth–Morris–Pratt algorithm is the most popular linear time algorithm for string matching. It is little difficult to understand and debug in real time contests. So most programmer’s have a precoded KMP in their kitty.

To understand the algorithm, you can either read it from Introduction to Algorithms (CLRS) or from the wikipedia page. Here’s a sample C++ code.

void preKMP(string pattern, int f[])
{
        int m = pattern.length(),k;
        f[0] = -1;
        for (int i = 1; i<m; i++)
        {
                k = f[i-1];
                while (k>=0)
                {
                        if (pattern[k]==pattern[i-1])
                                break;
                        else
                                k = f[k];
                }
                f[i] = k + 1;
        }
}
 
bool KMP(string pattern, string target)
{ 
        int m = pattern.length();
        int n = target.length();
        int f[m];
        
        preKMP(pattern, f);
        
        int i = 0;
        int k = 0;
        
        while (i<n)
        {
                if (k==-1)
                {
                        i++;
                        k = 0;
                }
                else if (target[i]==pattern[k])
                {
                        i++;
                        k++;
                        if (k==m)
                                return 1;
                }
                else
                        k=f[k];
        }
        return 0;
}

NJOY!
-fR0DDY

Evaluation of Powers

This is a very interesting problem with a lots of history. Anyways we will not wonder into it. We shall see how fast can we calculate xⁿ, given x and n where n is a positive integer. The brute force method would be to run a loop from 2 to n and calculate in n-1 steps. We will discuss three methods to do it quickly.

Binary Method
This the most common method used in programs today. It is also called the Dynamic Programming method. Here is an C++ implementation :

int binary(int x,int n)
{
    if (n==1)
       return x;
    if (n%2==0)
    {
       int t=binary(x,n/2);
       return t*t;
    }
    else
        return x*binary(x,n-1);
}

But does this method give the minimum number of multiplications. The answer is NO.
The smallest counterexample is n=15. The binary method takes six multiplications but the best method can do it in five multiplications. We can calculate y = x³ in two multiplications and x¹⁵ = y⁵ in three more, needing only five multiplications in total.

Factor Method
Let n=pq where p is smallest prime factor of n. We can calculate n by first calculating p and then raising this quantity to q-th power. If n is prime we calculate x^n-1 and multiply by x. For example to calculate x⁵⁵, we first calculate y = x⁵ = x⁴x = (x²)²x; then we form y¹¹ = y¹⁰y = (y²)⁵y. The whole process takes eight multiplications.
But does this method give the minimum number of multiplications. The answer is NO.
The smallest counterexample is n=33. The factor method takes seven multiplications but the best method(binary method) can do it in six multiplications.

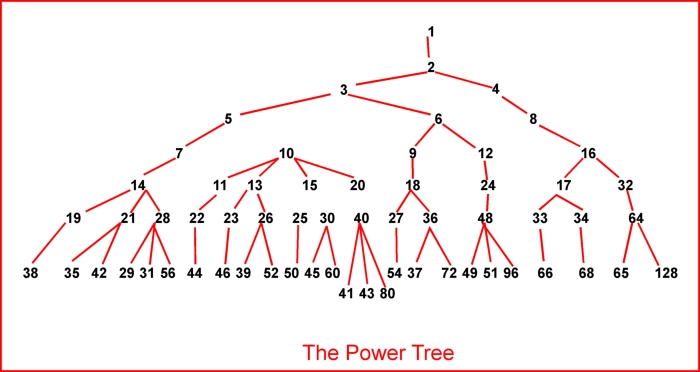
The “Power Tree Method”
Lets first see the power tree.

The "power tree"

Figure above shows the first few levels of the “power tree.” The (k + 1)-st level of this tree is defined as follows, assuming that the first k levels have been constructed: Take each node n of the lath level, from left to right in turn, and attach below it the nodes
                              n + 1, n + a₁, n + a₂, . . . , n + a_k-1 = 2n
(in this order), where 1, a₁, a₂, . . . , a₂ is the path from the root of the tree to n;but discard any node that duplicates a number that has already appeared in the tree. The C++ implementation of the above can be :

/** LINKU[j], LINKR[j] for 0 <= j <= 2^r;  
   point upwards and to the right, respectively,  
   if j is a number in the tree  
**/  
int LINKU[2050]={0},k=0,LINKR[2050]={0},q,s,nm,m,i,n;   
LINKR[0]=1;   
LINKR[1]=0;   
//11 being number of level   
while (k < 11)   
{   
    n=LINKR[0];m=0;   
    do  
    {   
        q=0,s=n;   
        do  
        {   
            if (LINKU[n+s]==0)   
            {   
                if (q==0)   
                   nm=n+s;   
                LINKR[n+s]=q;   
                LINKU[n+s]=n;   
                q=n+s;   
            }   
            s=LINKU[s];   
        }while (s!=0);   
        if (q!=0)   
        {   
            LINKR[m]=q;   
            m=nm;   
        }   
        n=LINKR[n];   
    }while (n!=0);   
    LINKR[m]=0;   
    k=k+1;   
}

But does this method give the minimum number of multiplications. The answer is NO.
The smallest counterexample is n=77.Other examples are 154 and 233.

Some Analysis

• The first case for which the power tree is superior to both the binary method and the factor method is 23.
• The first case for which the factor method beats the power tree method is 19879 = 103*193. Such cases are rare, only 6 for n<10⁵.
• Power tree never gives more multiplications for the computation of xⁿ than the binary method.

---

If You are not interested in Maths stop reading here.

Let l(n) denote the minimum number of multiplications for a given number n.
λ(n) = floor(lg n), where floor(x) is the largest integer not greater than x.
v(n) = number of 1s in the binary representation of n.

They follow the following recurrence relations :

λ(1)=0, λ(2n) = λ(2n+1) = λ(n) + 1;
v(1)=1, v(2n)=v(n), v(2n+1) = v(n)+1.

The binary method requires λ(n) + v(n) – 1  steps.

So we have following theorems

• l(n)<= λ(n) + v(n) -1.
• l(n)>= ceiling(lg n), where ceiling(x) is the smallest integer not less than x.
• l(2^A) = A.
• l(2^A + 2^B) = A+1 if A>B.
• l(2^A + 2^B + 2^C) = A+2 if A>B>C.

Conjecture

• l(2n) = l(n) +1; It fails since l(191) = l(382) = 11.
• The smallest four values for which l(2n) = l(n) are n = 191,701,743,1111.

Conclusion

The table of l(n) may be prepared for 2<=n<=1000 by using the formula l(n) = min(l(n-1)+1 , l_n) – δ_n,
where l_n = ∞ if n is prime, otherwise l_n = l(p)+l(n/p) if p is the smallest prime dividing n; and δ_n = 1 for n in Table below and 0 otherwise.

23
163
229
319
371
413
453
553
599
645
707
741
813
849
903


43
165
233
323
373
419
455
557
611
659
709
749
825
863
905


59
179
281
347
377
421
457
561
619
667
711
759
835
869
923


77
203
283
349
381
423
479
569
623
669
713
779
837
887
941


83
211
293
355
382
429
503
571
631
677
715
787
839
893
947


107
213
311
359
395
437
509
573
637
683
717
803
841
899
955


149
227
317
367
403
451
551
581
643
691
739
809
845
901
983

Phew!!! That was long.

-fR0D
(notes from TAOCP written by Donald E Knuth)

---

Links :
http://www.research.att.com/~njas/sequences/a003313.txt
http://wwwhomes.uni-bielefeld.de/achim/addition_chain.html

Binary GCD Algorithm

Most of us know that to find the GCD of two numbers, Euclid Algorithm is the best algorithm. But thanks to Josef Stein, there is the Binary GCD Algorithm which is touch faster than the Euclid’s Algorithm.

The Euclids Algorithm implemented is :

long long gcd(long long a, long long b)
{
    if(a==0) return(b);
    return(gcd(b%a, a));
}

The Binary GCD Algorithm as given in the The Art of Computer Programming written by D.E.Knuth is as follows :

Given positive integers u and v,
this algorithm finds their greatest common divisor.
A1. [Find power of 2.] Set k←0, and then repeatedly set k← k + 1, 
u ← u/2,v ← v/2, zero or more times until u and v are not both even.
A2. [Initialize.] (Now the original values of u and v have 
been divided by 2^k,and at least one of their present values is odd.)
If u is odd, set t  ← -v, and go to A4. Otherwise set t ← u.
A3. [Halve t.] (At this point, t is even, and nonzero.) Set t ← t/2.
A4. [Is t even?] If t is even, go back to A3.
A5. [Reset max(u, v).] If t > 0, set u ← t; otherwise set v←  -t.
(The larger of u and v has been replaced by |t|,
except perhaps during the first time this step is performed.)
A6. [Subtract.] Set t ← u-v. If t != 0, go back to A3.
Otherwise the algorithm terminates with u* 2^k as the output.

Implementation in C++ would look something like this :
int binarygcd(int u,int v)
{
int k=0,t=0,i;
while (!(u&1) && !(v&1))
{
k++;
u>>=1;
v>>=1;
}
if (u&1)
t=u;
else
t=-v;
do
{
while (!(t&1))
t>>=1;
if (t>0)
u=t;
else
v=-t;
t=u-v;
}while (t);
for (i=0;i