Recurrence Relation and Matrix Exponentiation

Recurrence relations appear many times in computer science. Using recurrence relation and dynamic programming we can calculate the n^th term in O(n) time. But many times we need to calculate the n^th in O(log n) time. This is where Matrix Exponentiation comes to rescue.

We will specifically look at linear recurrences. A linear recurrence is a sequence of vectors defined by the equation X_i+1 = M X_i for some constant matrix M. So our aim is to find this constant matrix M, for a given recurrence relation.

Let’s first start by looking at the common structure of our three matrices X_i+1, X_i and M. For a recurrence relation where the next term is dependent on last k terms, X_i+1 and X_i+1 are matrices of size 1 x k and M is a matrix of size k x k.

| f(n+1)   |       | f(n)   |
|  f(n)    |       | f(n-1) |
| f(n-1)   | = M x | f(n-2) |
| ......   |       | ...... |
| f(n-k+1) |       | f(n-k) |

Let’s look at different type of recurrence relations and how to find M.

1. Let’s start with the most common recurrence relation in computer science, The Fibonacci Sequence. F_i+1 = F_i + F_i-1.

| f(n+1) | = M x | f(n)   |
| f(n)   |       | f(n-1) |

Now we know that M is a 2 x 2 matrix. Let it be

| f(n+1) | = | a b | x | f(n)   |
| f(n)   |   | c d |   | f(n-1) |

Now a*f(n) + b*f(n-1) = f(n+1) and c*f(n) + d*f(n-1) = f(n). Solving these two equations we get a=1,b=1,c=1 and d=0. So,

| f(n+1) | = | 1 1 | x | f(n)   |
| f(n)   |   | 1 0 |   | f(n-1) |

2. For recurrence relation f(n) = a*f(n-1) + b*f(n-2) + c*f(n-3), we get

| f(n+1) | = | a b c | x | f(n)   |
| f(n)   |   | 1 0 0 |   | f(n-1) |
| f(n-1) |   | 0 1 0 |   | f(n-2) |

3. What if the recurrence relation is f(n) = a*f(n-1) + b*f(n-2) + c, where c is a constant. We can also add it in the matrices as a state.

| f(n+1) | = | a b 1 | x | f(n)   |
| f(n)   |   | 1 0 0 |   | f(n-1) |
| c      |   | 0 0 1 |   | c      |

4. If a recurrence relation is given like this f(n) = f(n-1) if n is odd, f(n-2) otherwise, we can convert it to f(n) = (n&1) * f(n-1) + (!(n&1)) * f(n-2) and substitute the value accordingly in the matrix.

5.If there are more than one recurrence relation, g(n) = a*g(n-1) + b*g(n-2) + c*f(n), and, f(n) = d*f(n-1) + e*f(n-2). We can still define the matrix X in following way

| g(n+1) |   | a b c 0 |   | g(n)   |
| g(n)   | = | 1 0 0 0 | x | g(n-1) |
| f(n+2) |   | 0 0 d e |   | f(n+1) |
| f(n+1) |   | 0 0 1 0 |   | f(n)   |

Now that we have got our matrix M, how are we going to find the nth term.
X_i+1 = M X_i
(Multiplying M both sides)
M * X_i+1 = M * M X_i
X_i+2 = M^2 X_i
..
X_i+k = M^k X_i

So all we need now is to find the matrix M^k to find the k-th term. For example in the case of Fibonacci Sequence,

M^2 = | 2 1 |
      | 1 1 |

Hence F(2) = 2.

Now we need to learn to find M^k in O(n³ log b) time. The brute force approach to calculate a^b takes O(b) time, but using a recursive divide-and-conquer algorithm takes only O(log b) time:

• If b = 0, then the answer is 1.
• If b = 2k is even, then a^b = (a^k)².
• If b is odd, then a^b = a * a^b-1.

We take a similar approach for Matrix Exponentiation. The multiplication part takes the O(n³) time and hence the overall complexity is O(n³ log b). Here’s a sample code in C++ using template class:

#include<iostream>
using namespace std;

template< class T >
class Matrix
{
    public:
		int m,n;
		T *data;

        Matrix( int m, int n );
		Matrix( const Matrix< T > &matrix );

		const Matrix< T > &operator=( const Matrix< T > &A );
        const Matrix< T > operator*( const Matrix< T > &A );
        const Matrix< T > operator^( int P );

		~Matrix();
};

template< class T >
Matrix< T >::Matrix( int m, int n )
{
    this->m = m;
    this->n = n;
    data = new T[m*n];
}

template< class T >
Matrix< T >::Matrix( const Matrix< T > &A )
{
    this->m = A.m;
    this->n = A.n;
    data = new T[m*n];
    for( int i = 0; i < m * n; i++ )
		data[i] = A.data[i];
}

template< class T >
Matrix< T >::~Matrix()
{
    delete [] data;
}

template< class T >
const Matrix< T > &Matrix< T >::operator=( const Matrix< T > &A )
{
    if( &A != this )
    {
        delete [] data;
        m = A.m;
        n = A.n;
        data = new T[m*n];
        for( int i = 0; i < m * n; i++ )
			data[i] = A.data[i];
    }
    return *this;
}

template< class T >
const Matrix< T > Matrix< T >::operator*( const Matrix< T > &A )
{
	Matrix C( m, A.n );
	for( int i = 0; i < m; ++i )
		for( int j = 0; j < A.n; ++j )
        {
			C.data[i*C.n+j]=0;
			for( int k = 0; k < n; ++k )
				C.data[i*C.n+j] = C.data[i*C.n+j] + data[i*n+k]*A.data[k*A.n+j];
		}
	return C;
}

template< class T >
const Matrix< T > Matrix< T >::operator^( int P )
{
	if( P == 1 ) return (*this);
	if( P & 1 ) return (*this) * ((*this) ^ (P-1));
	Matrix B = (*this) ^ (P/2);
	return B*B;
}

int main()
{
    Matrix<int> M(2,2);
    M.data[0] = 1;M.data[1] = 1;
    M.data[2] = 1;M.data[3] = 0;

	int F[2]={0,1};
    int N;
	while (~scanf("%d",&N))
		if (N>1)
			printf("%lld\n",(M^N).data[0]);
		else
			printf("%d\n",F[N]);
}

Knuth–Morris–Pratt Algorithm (KMP)

Knuth–Morris–Pratt algorithm is the most popular linear time algorithm for string matching. It is little difficult to understand and debug in real time contests. So most programmer’s have a precoded KMP in their kitty.

To understand the algorithm, you can either read it from Introduction to Algorithms (CLRS) or from the wikipedia page. Here’s a sample C++ code.

void preKMP(string pattern, int f[])
{
        int m = pattern.length(),k;
        f[0] = -1;
        for (int i = 1; i<m; i++)
        {
                k = f[i-1];
                while (k>=0)
                {
                        if (pattern[k]==pattern[i-1])
                                break;
                        else
                                k = f[k];
                }
                f[i] = k + 1;
        }
}
 
bool KMP(string pattern, string target)
{ 
        int m = pattern.length();
        int n = target.length();
        int f[m];
        
        preKMP(pattern, f);
        
        int i = 0;
        int k = 0;
        
        while (i<n)
        {
                if (k==-1)
                {
                        i++;
                        k = 0;
                }
                else if (target[i]==pattern[k])
                {
                        i++;
                        k++;
                        if (k==m)
                                return 1;
                }
                else
                        k=f[k];
        }
        return 0;
}

NJOY!
-fR0DDY

The Z Algorithm

In this post we will discuss an algorithm for linear time string matching. It is easy to understand and code and is usefull in contests where you cannot copy paste code.

Let our string be denoted by S.
z[i] denotes the length of the longest substring of S that starts at i and is a prefix of S.
α denotes the substring.
r denotes the index of the last character of α and l denotes the left end of α.

To find whether a pattern(P) of length n is present in a target string(T) of length m, we will create a new string S = P$T where $ is a character present neither in P nor in T. The space taken is n+m+1 or O(m). We will compute z[i] for all i such that 0 < i < n+m+1. If z[i] is equal to n then we have found a occurrence of P at position i – n – 1. So we can all the occurrence of P in T in O(m) time. To calculate z[i] we will use the z algorithm.

The Z Algorithm can be read from the section 1.3-1.5 of book Algorithms on strings, trees, and sequences by Gusfield. Here is a sample C++ code.

bool zAlgorithm(string pattern, string target)
{
	string s = pattern + '$' + target ;
	int n = s.length();
	vector<int> z(n,0);
	
	int goal = pattern.length();
	int r = 0, l = 0, i;
	for (int k = 1; k<n; k++)
	{
		if (k>r)
		{
			for (i = k; i<n && s[i]==s[i-k]; i++);
			if (i>k)
			{
				z[k] = i - k;
				l = k;
				r = i - 1;
			}
		}
		else
		{
			int kt = k - l, b = r - k + 1;
			if (z[kt]>b)
			{
				for (i = r + 1; i<n && s[i]==s[i-k]; i++);
				z[k] = i - k;
				l = k;
				r = i - 1;
			}
		}
		if (z[k]==goal)
			return true;
	}
	return false;
}

NJOY!
-fR0D

Binary Indexed Tree (BIT)

In this post we will discuss the Binary Indexed Trees structure. According to Peter M. Fenwick, this structure was first used for data compression. Let’s define the following problem: We have n boxes. Possible queries are

1. Add marble to box i
2. Return sum of marbles from box k to box l

The naive solution has time complexity of O(1) for query 1 and O(n) for query 2. Suppose we make m queries. The worst case (when all queries are 2) has time complexity O(n * m). Binary Indexed Trees are easy to code and have worst time complexity O(m log n).

The two major functions are

• update (idx,val) : increases the frequency of index idx with the value val
• read (idx) : reads the cumulative frequency of index idx

Note : tree[idx] is sum of frequencies from index (idx – 2^r + 1) to index idx where r is rightmost position of 1 in the binary notation of idx, f is frequency of index, c is cumulative frequency of index, tree is value stored in tree data structure.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
f	1	0	2	1	1	3	0	4	2	5	2	2	3	1	0	2
c	1	1	3	4	5	8	8	12	14	19	21	23	26	27	27	29
tree	1	1	2	4	1	4	0	12	2	7	2	11	3	4	0	29

Table 1.1

 

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
tree	1	1..2	3	1..4	5	5..6	7	1..8	9	9..10	11	9..12	13	13..14	15	1..16

Table 1.2 – table of responsibility

Here’s a C++ template code :

#include<iostream>
using namespace std;

template<class T>
class BIT
{
      T *tree;
      int maxVal;
      public:
      BIT(int N)
      {
              tree = new T[N+1];
              memset(tree,0,sizeof(T)*(N+1));
              maxVal = N;
      }
      void update(int idx, T val)
      {
           while (idx <= maxVal)
           {
                 tree[idx] += val;
                 idx += (idx & -idx);
           }
      }
      //Returns the cumulative frequency of index idx
      T read(int idx)
      {
        T sum=0;
        while (idx>0)
        {
              sum += tree[idx];
              idx -= (idx & -idx);
        }
        return sum;
      }
};

int main()
{
    int a[100],cur=1,mul=2,add=19,MAX=65536,x,i;
    //Initialize the size by the
    //maximum value the tree can have
    BIT<int> B(MAX);
    for (i=0;i<50;i++)
    {
        a[i] = cur;
        B.update(a[i],1);
        cur = ((cur * mul + add) % MAX);
    }
    while (cin>>x)
    {
          cout<<B.read(x)<<endl;
    }

}

Resources:

1. Topcoder Tutorial

NJOY!
-fR0D

Segment Trees

A segment tree is a heap-like data structure that can be used for making update/query operations upon array intervals in logarithmical time. We define the segment tree for the interval [i, j] in the following recursive manner:

• the first node will hold the information for the interval [i, j]
• if i<j the left and right son will hold the information for the intervals [i, (i+j)/2] and [(i+j)/2+1, j]

See the picture below to understand more :

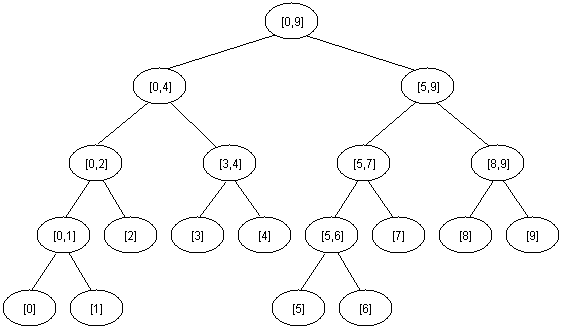
Segment Tree

We can use segment trees to solve Range Minimum/Maximum Query Problems (RMQ). The time complexity is T(N, log N) where O(N) is the time required to build the tree and each query takes O(log N) time. Here’s a C++ template implementation :

#include<iostream>
using namespace std;
#include<math.h>

template<class T>
class SegmentTree
{
     int *A,size;
     public:
     SegmentTree(int N)
     {
          int x = (int)(ceil(log2(N)))+1;
          size = 2*(int)pow(2,x);
          A = new int[size];
          memset(A,-1,sizeof(A));
     }
     void initialize(int node, int start,
                         int end, T *array)
     {

          if (start==end)
             A[node] = start;
          else
          {
              int mid = (start+end)/2;
              initialize(2*node,start,mid,array);
              initialize(2*node+1,mid+1,end,array);
              if (array[A[2*node]]<=
                     array[A[2*node+1]])
                 A[node] = A[2 * node];
              else
                  A[node] = A[2 * node + 1];
          }
     }
     int query(int node, int start,
                   int end, int i, int j, T *array)
     {
         int id1,id2;
         if (i>end || j<start)
            return -1;

         if (start>=i && end<=j)
            return A[node];

         int mid = (start+end)/2;
         id1 = query(2*node,start,mid,i,j,array);
         id2 = query(2*node+1,mid+1,end,i,j,array);

         if (id1==-1)
            return id2;
         if (id2==-1)
            return id1;

         if (array[id1]<=array[id2])
            return id1;
         else
             return id2;
     }
};

int main()
{
    int i,j,N;
    int A[1000];
    scanf("%d",&N);
    for (i=0;i<N;i++)
        scanf("%d",&A[i]);

    SegmentTree<int> s(N);
    s.initialize(1,0,N-1,A);
    while (scanf("%d%d",&i,&j)!=EOF)
      printf("%d\n",A[s.query(1,0,N-1,i-1,j-1,A)]);
}

Resources:

1. Topcoder Tutorial

NJOY!
-fR0D

Longest Increasing Subsequence (LIS)

The longest increasing subsequence problem is to find a subsequence of a given sequence in which the subsequence elements are in sorted order, lowest to highest, and in which the subsequence is as long as possible. This subsequence is not necessarily contiguous.
For example for the sequence -7 10 9 2 3 8 8 1 the longest (strictly) increasing subsequence is -7 2 3 8 of length 4.

There are few methods to solve this question. The very first method is to sort the given sequence and save it into another array and then take out the longest common subsequence of the two arrays. This method has a complexity of O(n²) which should be good for most question but not all.

We will see here an algorithm which take O(n log k) time where k is the size of the LIS. For explanation on this algorithm see Faster Algorithm on this page. Here’s a small code to calculate only the length of the LIS.

#include<iostream>
#include<set>
#include<vector>
using namespace std;

int LIS(vector<int> A)
{
    int N = A.size(),i;
    set<int> s;
    set<int>::iterator k;
    for (i=0;i<N;i++)
    {
        if (s.insert(A&#91;i&#93;).second)
        {
           k = s.find(A&#91;i&#93;);
           k++;
           if (k!=s.end())
              s.erase(k);
        }
    }
    return s.size();
}&#91;/sourcecode&#93;
To also get the LIS we need to maintain a previous array which stores the index of the previous element in the LIS. Here's a C++ implementation. It returns the LIS as an array.
&#91;sourcecode language='cpp'&#93;#include<iostream>
#include<map>
#include<vector>
using namespace std;

typedef pair < int , int > PI;

vector<int> LIS(vector<int> A)
{
    int N = A.size(),i,j=-1,t;
    vector<int> pre(N,-1),res;
    map<int,int> m;
    map<int,int>::iterator k,l;
    for (i=0;i<N;i++)
    {
        if (m.insert(PI(A&#91;i&#93;,i)).second)
        {
           k = m.find(A&#91;i&#93;);
           l = k;
           k++;
           if (l==m.begin())
                  pre&#91;i&#93;=-1;
           else
           {
               l--;
               pre&#91;i&#93;=l->second;
           }
           if (k!=m.end())
              m.erase(k);
        }
    }
    k=m.end();
    k--;
    j = k->second;
    while (j!=-1)
    {
          res.push_back(A[j]);
          j = pre[j];
    }
    reverse (res.begin(),res.end());
    return res;
}

Note that if there are more than one LIS the above code prints the last one which occured in the input array. Also to get the LDS we just need to change the lines :

set<int> s;
to
set<int,greater<int> > s;
and 
map<int,int> m;
to
map<int,int,greater<int> > m;

Also little changes need to be made to the above codes if you dont want the LIS to be strictly increasing and rather be Longest Non-Decreasing Subsequence or Longest Non-Increasing Subsequence.

Happy Coding!
-fR0D

Range Minimum Query

RANGE QUERY

Given a (big) array r[0..n-1], and a lot of queries of certain type. We may want to pre-process the data so that each query can be performed fast. In this section, we use T (f, g) to denote the running time for an algorithm is O(f(n)) for pre-processing, and O(g(n)) for each query.

If the queries are of type getsum(a, b), which asks the sum of all the elements between a and b, inclusive, we have a T (n, 1) algorithm: Compute s[i] to be the sum from r[0] to r[i-1], inclusive, then getsum(a,b) simply returns s[b+1]-s[a].

RANGE MINIMUM QUERY

For the queries of the form getmin(a,b) asks the minimum elements between r[a] and r[b], inclusive, the task is little more hard. The idea is always to get the min in some big ranges, so in the queries we may try to use these big ranges to compute fast. One simple algorithm is T (n,sqrt(n)): Break the n numbers into sqrt(n) regions, each of size sqrt(n). Compute the champion for each region. For each query getmin(a,b), we go from a towards right to the nearest station (at most sqrt(n) steps), then go by at most sqrt(n) stations (big regions) to the nearest station before b, and from there go to b.

Sparse Table (ST) Algorithm

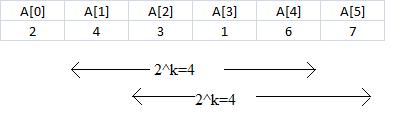
A better approach is to preprocess RMQ for sub arrays of length 2^k using dynamic programming. We will keep an array preProcess[0, N-1][0, logN] where preProcess[i][j] is the index of the minimum value in the sub array starting at i having length 2^j. For example :

A[0]	A[1]	A[2]	A[3]	A[4]	A[5]
2	4	3	1	6	7

For the above array the preProcess[1][0] = 1, preProcess[1][1]=2,preProcess[1][2]=3 and so on. Specifically, we find the minimum in a block of size 2^j by comparing the two minima of its two constituent blocks of size 2^j-1. More formally, preProcess[i, j] = preProcess[i, j -1] if A[preProcess[i, j -1]] <= A[preProcess[i+2^j-1, j -1]] and preProcess[i, j] = preProcess[i+2^j-1, j -1] otherwise.

Once we have these values preprocessed, let’s show how we can use them to calculate RMQ(i, j). The idea is to select two blocks that entirely cover the interval [i..j] and  find the minimum between them. We select two overlapping blocks that entirely cover the subrange: let 2k be the size of the largest block that fits into the range from i to j, that is let k = log(j – i). Then rmq(i, j) can be computed by comparing the minima of the following two blocks: i to i + 2^k – 1 (preProcess(i, k)) and j – 2^k + 1 to j (preProcess(j –2^k +1, k)). These values have already been computed, so we can find the RMQ in constant time.

So as shown above if we need to calculate minimum between A[1] and A[5] we will take two sections of size 4 and compare their minimum values to get the answer. Below is a C++ template class implementation :

int preProcess[1000][10];
template
class RMQMin
{
  T *A;
  public:
    RMQMin(int N,T *array):A(array)
    {
        int i,j;
        for (i=0;i<N;i++)
            preProcess[i][0]=i;
        for (j=1; (1<<j)<=N; j++)
            for (i=0; i+(1<<j)-1<N; i++)
                preProcess[i][j]=
                A[preProcess[i][j-1]]<=
                A[preProcess[i+(1<<(j-1))][j-1]]?
                preProcess[i][j-1]
                :preProcess[i+(1<<(j-1))][j-1];
    }
   
    int query(int start,int end)
    {
        int diff=end-start;
        diff=31 - __builtin_clz(diff+1);
        return A[preProcess[start][diff]]
          <=A[preProcess[end-(1<<diff)+1][diff]]?
          preProcess[start][diff]
          :preProcess[end-(1<<diff)+1][diff];
    }
};

You can simply use the above class for any type of variable(numeric ofcourse). Just keep in mind that you have to declare a preProcess array of size N x log N . So it turns out that the space complexity of the algorithm is O(N log N) and time complexity T(NlogN, 1).

-fR0D

Google Interview Questions

All the below questions are to be done in O(n) time complexity.

1>Given an array of size n-1 whose entries are integers in the range [1, n], find an integer that is missing. Use only O(1) space and treat the input as read-only.

2>Given an array of size n-2 whose entries are integers in the range [1, n], find two integer that are missing.

3>There is an array A[N] of N integers. You have to compose an array B[N] such that Output[i] will be equal to the product of all the elements of A[] except A[i].

or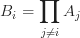
Example:
INPUT:[4, 3, 2, 1, 2]
OUTPUT:[12, 16, 24, 48, 24]

Solve it without division operator and in O(n).

Solution :

1>Let the missing number be M. We know that the sum of first N natural numbers is N*(N+1)/2. Traverse through the array once and calculate the sum. This is the sum of First N natural numbers – M or S=N*(N+1)/2 – M. Therefore M = N*(N+1)/2 – S.

2>Similar approach to the first one. Traverse the array once and calculate its sum and multiplication. Let the sum be S and multiplication be M. Let the missing numbers be P and Q. From above we know that P+Q = N*(N+1)/2 – S. Also P*Q = N!/M. So we can get P and Q from these two equations.

3> Lets first see the C++ solution.
void solution(vector A)
{  
    int N=A.size(),i,j;
    vector L(N,0);
    vector R(N,0);
    vector B(N,0);
    for (i=0,j=N-1; i=0 ;i++, j–)
    {  
        L[i] = i==0? 1 : A[i-1] * L[i-1];  
        R[j] = j==N-1? 1 : R[j+1] * A[j+1];  
    }  
   
    for (i=0; i